Actualités

Laissez-moi vous parler de mon addiction. À une époque, je passais des heures sur un jeu appelé Mots de lettres. Si vous ne connaissez pas, le concept est simple : il faut former des mots à partir de cinq lettres données. Sur le papier, ça paraît facile, mais en réalité, ce jeu est tellement addictif qu’on y passe un temps fou sans même s’en rendre compte ! J’enchaînais facilement 2 à 3 heures par jour, à essayer toutes les combinaisons possibles avec ce même tas de lettres. À force, j’ai vraiment eu l’impression de gâcher mon temps là-dessus.

Déterminé à reprendre le contrôle, j’ai décidé de créer une solution qui m’aiderait à trouver tous les mots en un clin d'œil, histoire d’aller à l’essentiel sans y passer des heures.

Une approche naïve pour trouver des mots

Ma première idée a été d’y aller franchement, sans trop de finesse : prendre les lettres, générer toutes les combinaisons possibles, et voir ce qui marche. Une méthode brute, certes, mais qui me semblait faisable à première vue, même si un escargot aurait sans doute trouvé ça un peu lent.

La méthode de recherche simple (ou comment empirer le problème)

J'ai donc pris mes cinq lettres et généré absolument toutes les combinaisons, de mots d’une lettre jusqu’à cinq, pour n’en manquer aucun. Ensuite, pour chaque combinaison, je vérifiais si ça existait dans le dictionnaire. Sur le papier, j’étais persuadé que ça ferait le job. Mais en pratique… pas du tout.

Pour visualiser, imaginons seulement trois lettres : A, B et C. Voici toutes les combinaisons que cette méthode va générer :

Avec seulement trois lettres, on arrive déjà à 13 combinaisons uniques. Ajoutez deux lettres, et on passe à 325 combinaisons ! Imaginer le temps nécessaire pour vérifier chacune d’elles dans le dictionnaire donne une idée de la lenteur du processus, car chaque combinaison doit passer au crible pour voir si elle constitue un mot. Résultat : le nombre de vérifications explose rapidement.

En gros,

• pour 3 éléments, on aurait 3 + 3.2 + 3.2.1

• pour 4 éléments, on aurait 4 + 4.3 + 4.3.2 + 4.3.2.1

• pour 5 éléments, on aurait 5 + 5.4 + 5.4.3 + 5.4.3.2 + 5.4.3.2.1

Le code de l’approche naïve

Voici le code de cette méthode brute :

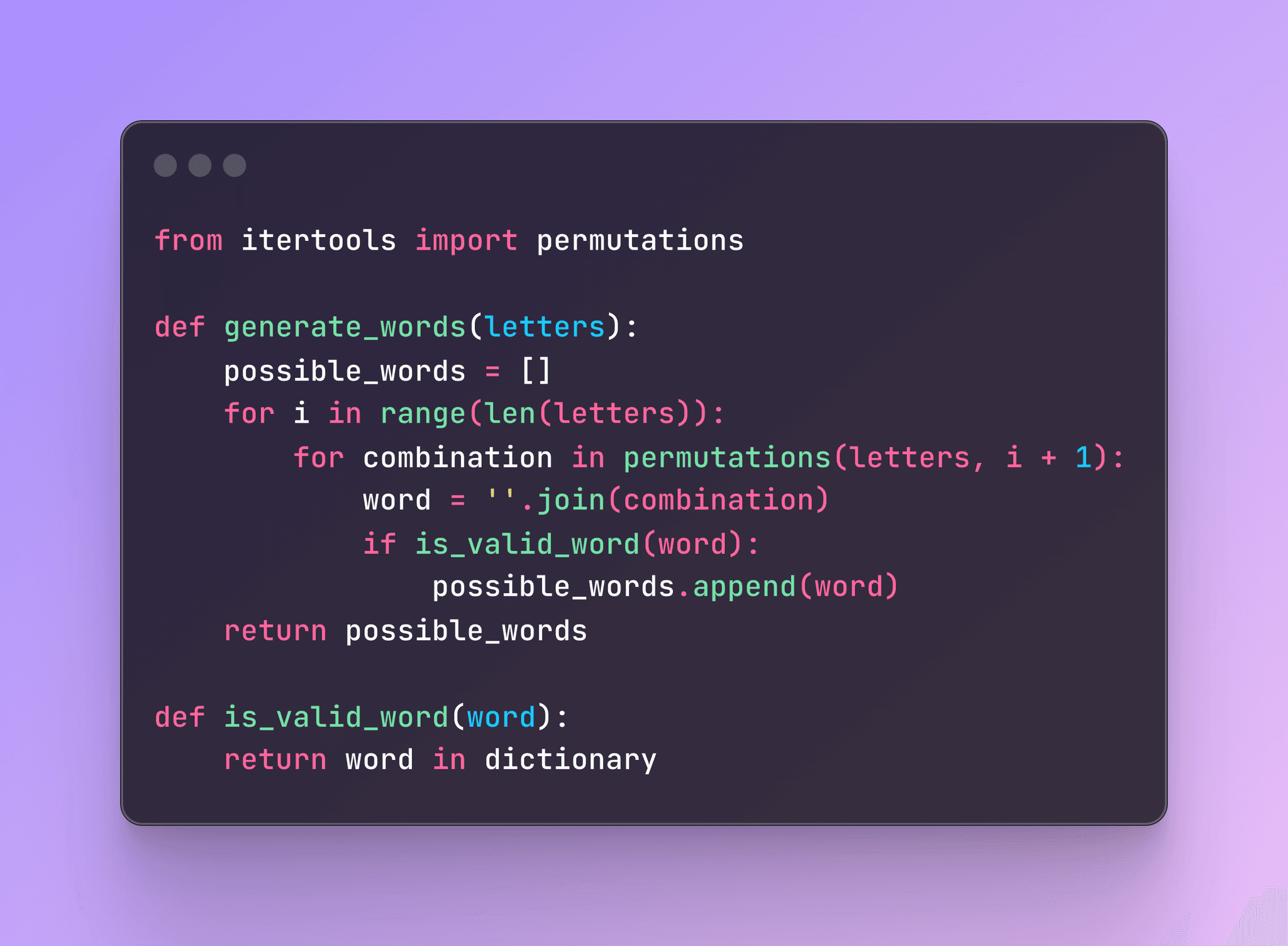
La complexité de l’approche

La complexité temporelle de cette méthode est de l’ordre de O(n*n!). Rapidement, j'ai constaté que cette méthode n'était pas juste un peu lente : c’était interminable, l'agonie ! Le PC chauffait, le ventilateur tournait comme si je minais de la crypto !

Une meilleure approche : le Trie

Il est temps d’aborder le Trie (prononcé « traille »). Oubliez la méthode naïve qui m’a fait perdre un temps précieux : le Trie, c’est comme passer du vélo à la moto de course. Cet algorithme permet de gérer les mots bien plus efficacement. Si j’avais découvert cette méthode plus tôt, j’aurais pu éviter les frustrations à répétition, en regardant mon ordinateur peiner sur chaque combinaison.

Qu’est-ce qu’un Trie ?

Selon Wikipédia, “ en informatique, un Trie ou arbre préfixe, est une structure de données ayant la forme d'un arbre enraciné. Il est utilisé pour stocker une table associative où les clés sont généralement des chaînes de caractères. Contrairement à un arbre binaire de recherche, aucun nœud dans le Trie ne stocke la chaîne à laquelle il est associé. C'est la position du nœud dans l'arbre qui détermine la chaîne correspondante. “

Comme souvent avec les définitions techniques, ça devient clair seulement si tu connais déjà le sujet... sinon, c'est du charabia !

Mais laissez-moi essayer de vous le rendre plus accessible.

Imaginez un Trie comme un arbre où chaque nœud représente une lettre d'un mot. On construit un chemin dans cet arbre pour chaque mot, en partant toujours de la racine. Ça vous permet de rechercher, ajouter ou vérifier l’existence de mots très rapidement. Et si vous voulez voir si un mot existe ou lister tous les mots qui partagent un préfixe, c’est presque trop facile : pas besoin de tester toutes les combinaisons, il suffit de suivre les chemins de l’arbre.

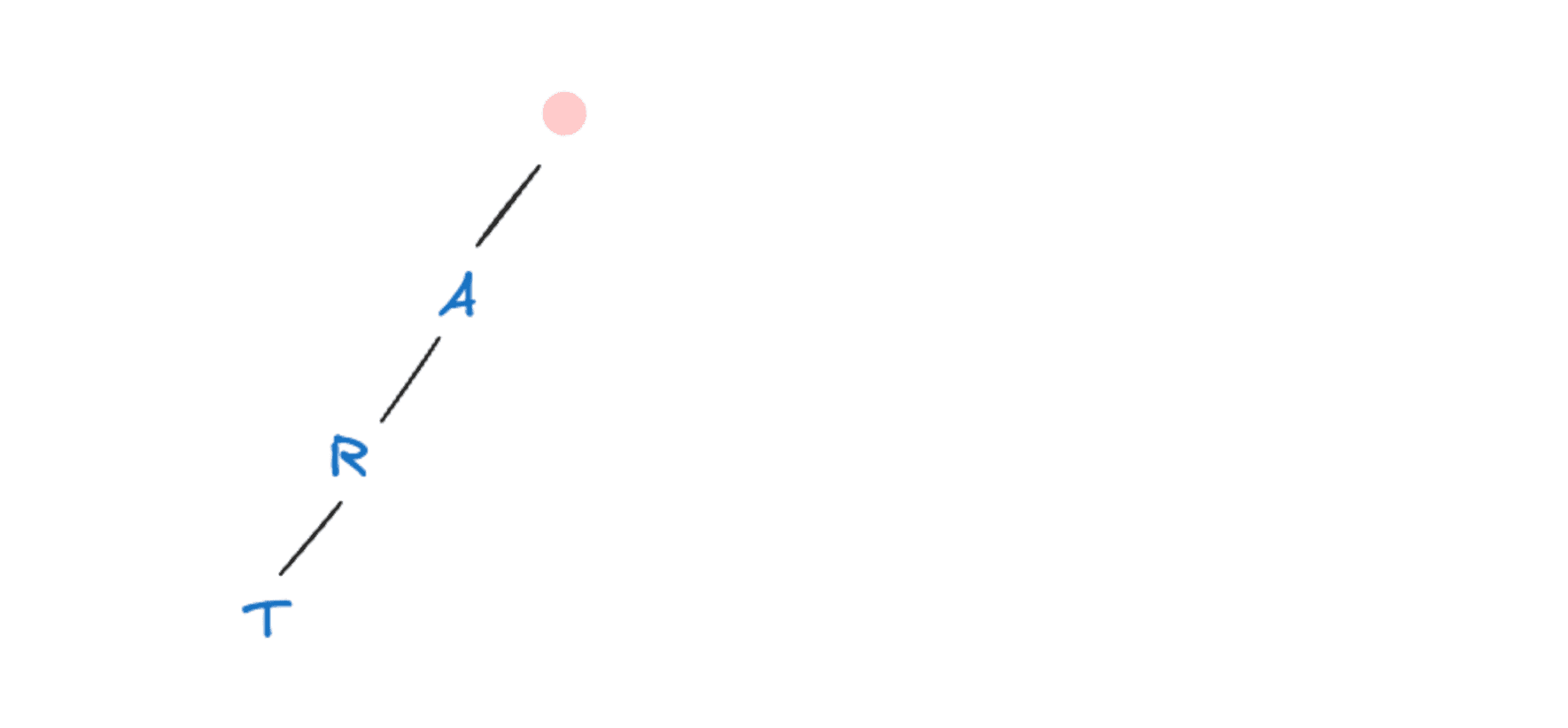
Imaginons un Trie où l’on insère des mots comme suit :

Initialement, l’arbre est vide et il ressemble à ça : 

Ensuite, on insère le mot "art" :

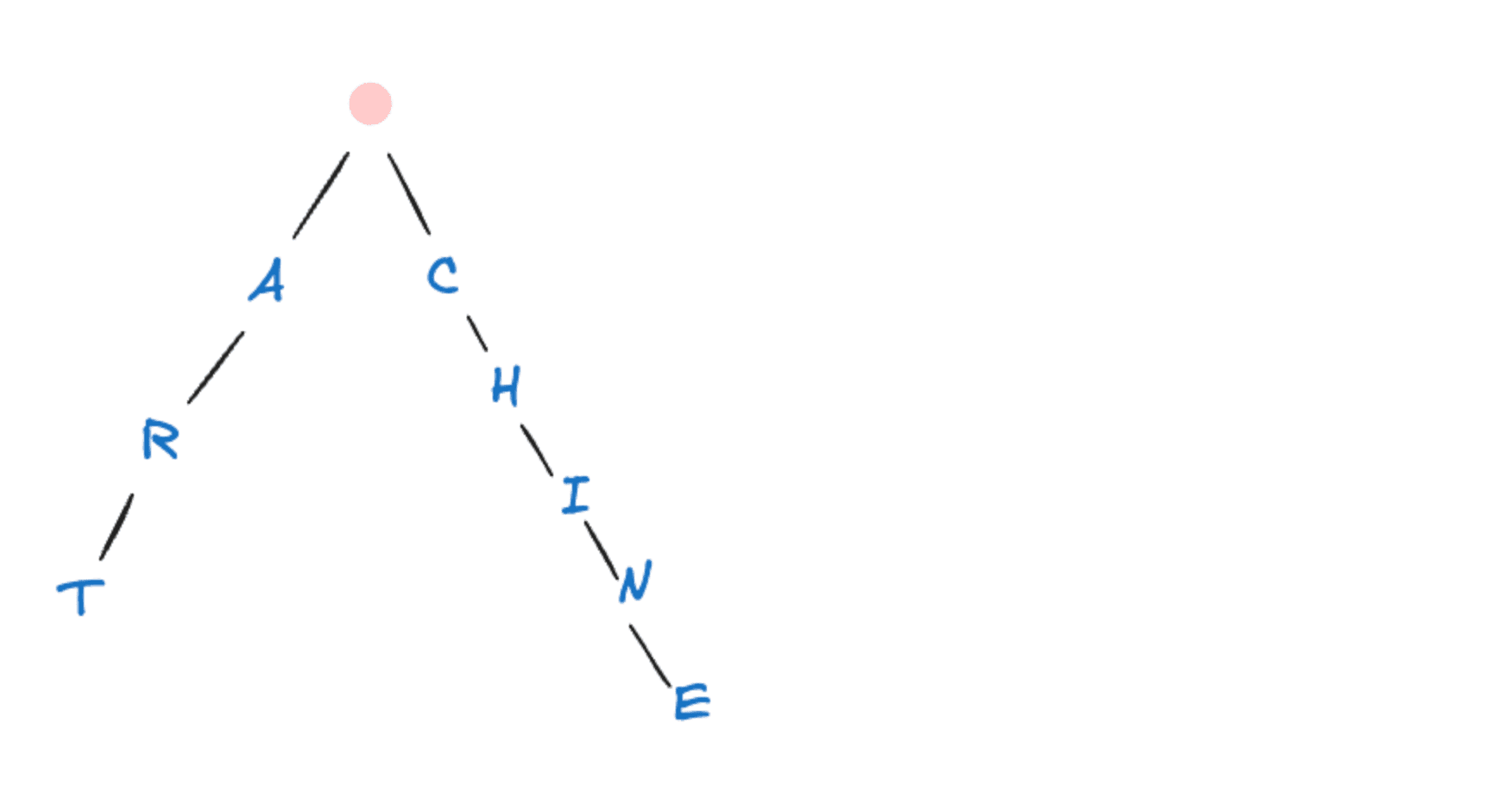
On insère le mot "chine" :

On insère le mot "chien" :

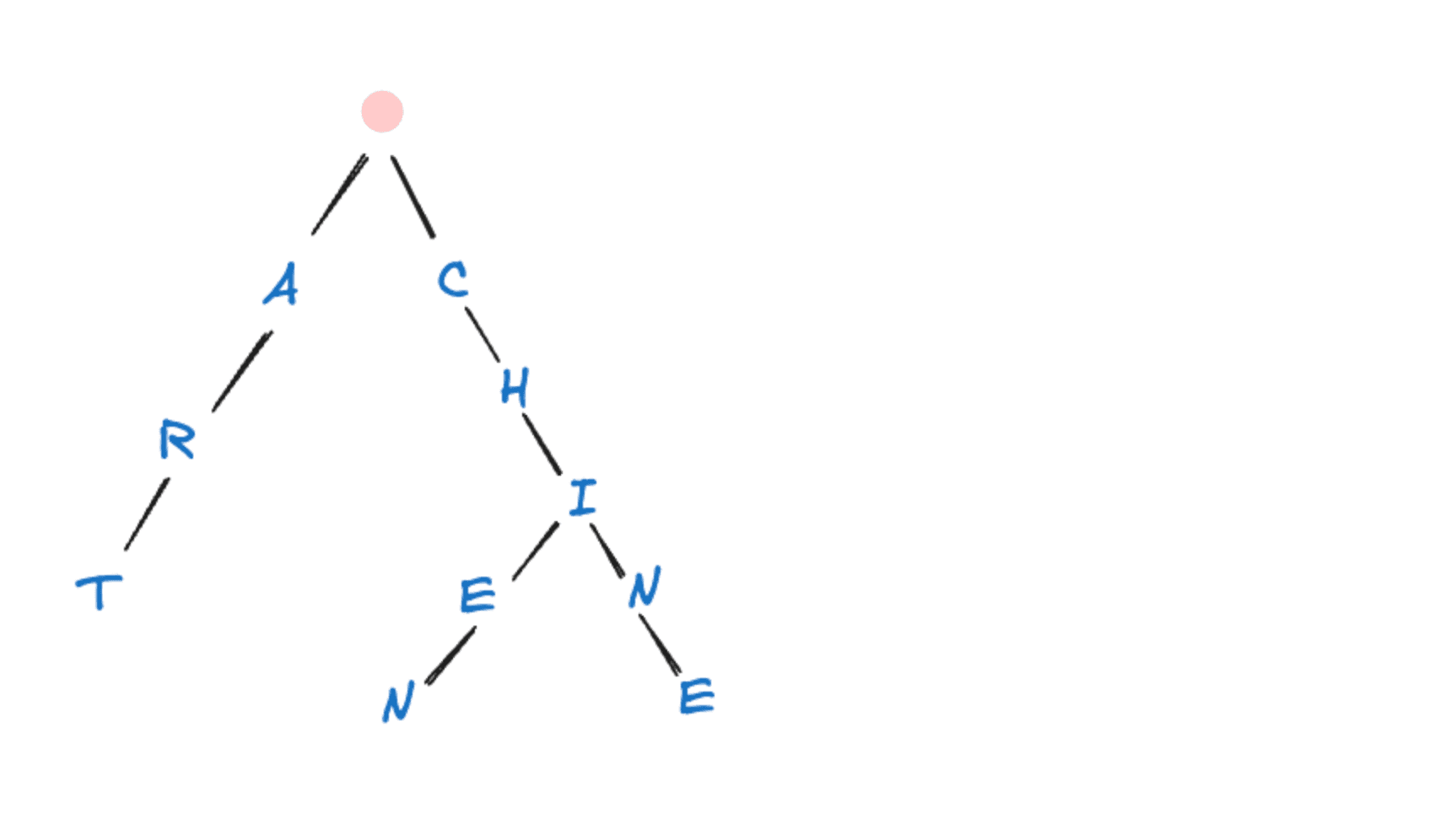
Dans un Trie, il devient très simple de vérifier si un préfixe existe (par exemple, "ch" est un préfixe commun à "chien" et "chine"). Toutes les sous-branches de "c-h" contiennent des mots qui commencent par "ch".

Pourquoi est-ce mieux ? 

Avec un Trie, vous pouvez effectuer des recherches par préfixe de manière très efficace. Lorsque vous cherchez un mot, vous commencez par vérifier si le préfixe existe. Si le préfixe est absent, inutile d'aller plus loin : aucun mot ne pourra commencer par cette suite de lettres. Cela vous permet d'éliminer immédiatement toutes les combinaisons associées à ce préfixe, ce qui fait gagner un temps précieux. Par exemple, si vous avez les lettres "N-E-H-I-C", et qu'il n'existe aucun mot débutant par "NH", inutile de vérifier toutes les combinaisons possibles (NHICE, NHIEC, etc.), soit 15 mots que vous n'avez même pas besoin de considérer.

En résumé, le Trie vous aide à filtrer les mots dès le départ, évitant les explorations de chemins inutiles. C'est une façon efficace de réduire l'espace de recherche et d'accélérer le processus, car vous vous concentrez uniquement sur les préfixes qui peuvent potentiellement former des mots valides.

Implémentation d'un Trie

Voici un aperçu de l'implémentation de cette approche :

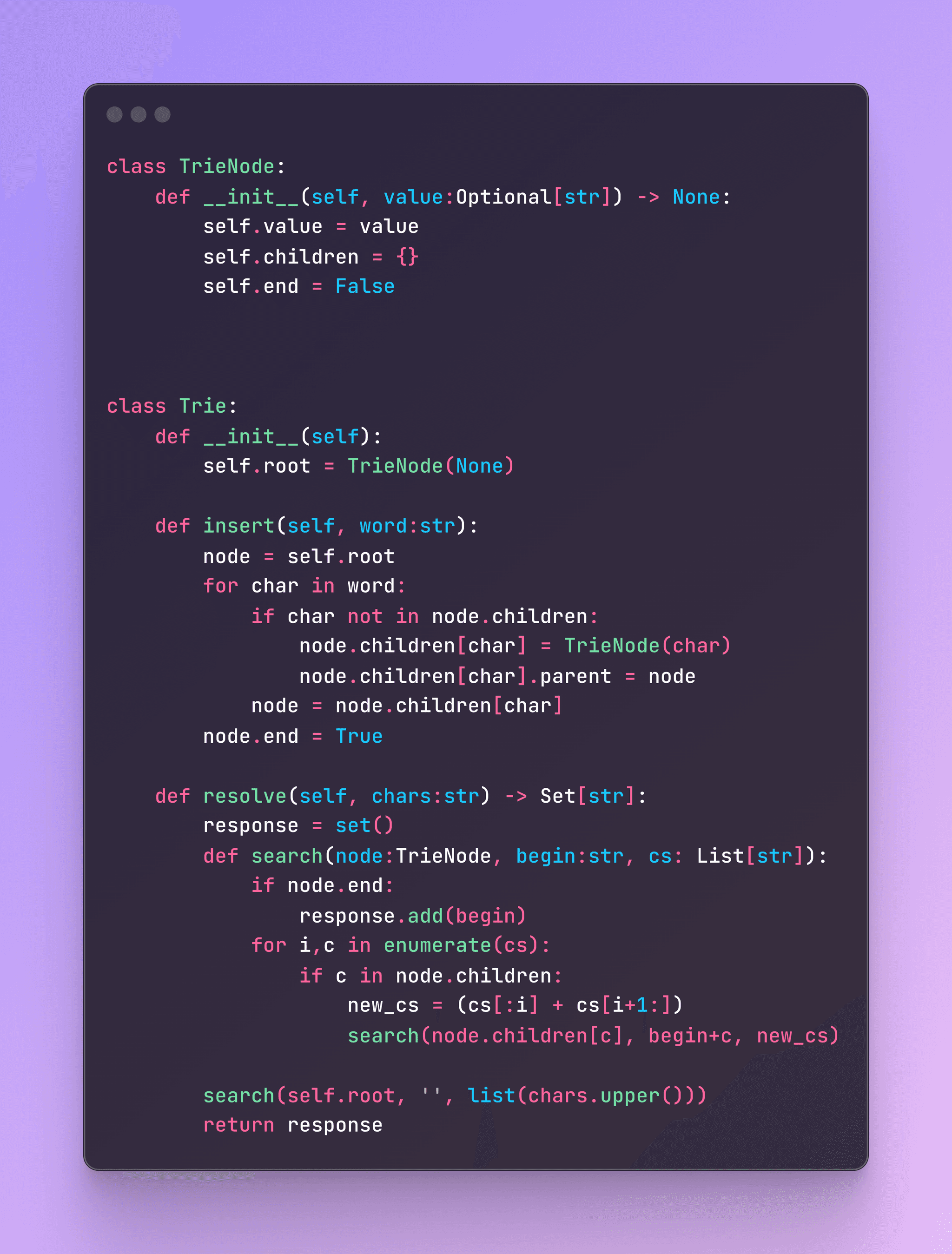
Ça fonctionne !!! Jeu terminé ! 🎉

Le temps libre, c’est ce petit espace précieux que l’on se crée au milieu du quotidien et de ses obligations. C’est le moment où on peut vraiment déconnecter, faire ce qu’on aime : plonger dans un bon bouquin, sortir avec les potes, ou juste s’affaler sur le canap’ pour binge-watcher une série. C’est un souffle de liberté qui nous rappelle qu’on n’est pas seulement des robots programmés pour bosser. En fait, ces moments de pause sont essentiels pour recharger les batteries, stimuler la créativité et garder le moral. Que ce soit une balade tranquille ou une soirée jeux vidéo, il faut en profiter à fond !

Trie vs. Approche naïve 

Après avoir mis en place mes deux solutions, il était temps de voir laquelle performait le mieux. Je me suis donc dit : « Allez, comparons la rapidité de mon algorithme de base avec celle du Trie. » Voici le verdict :

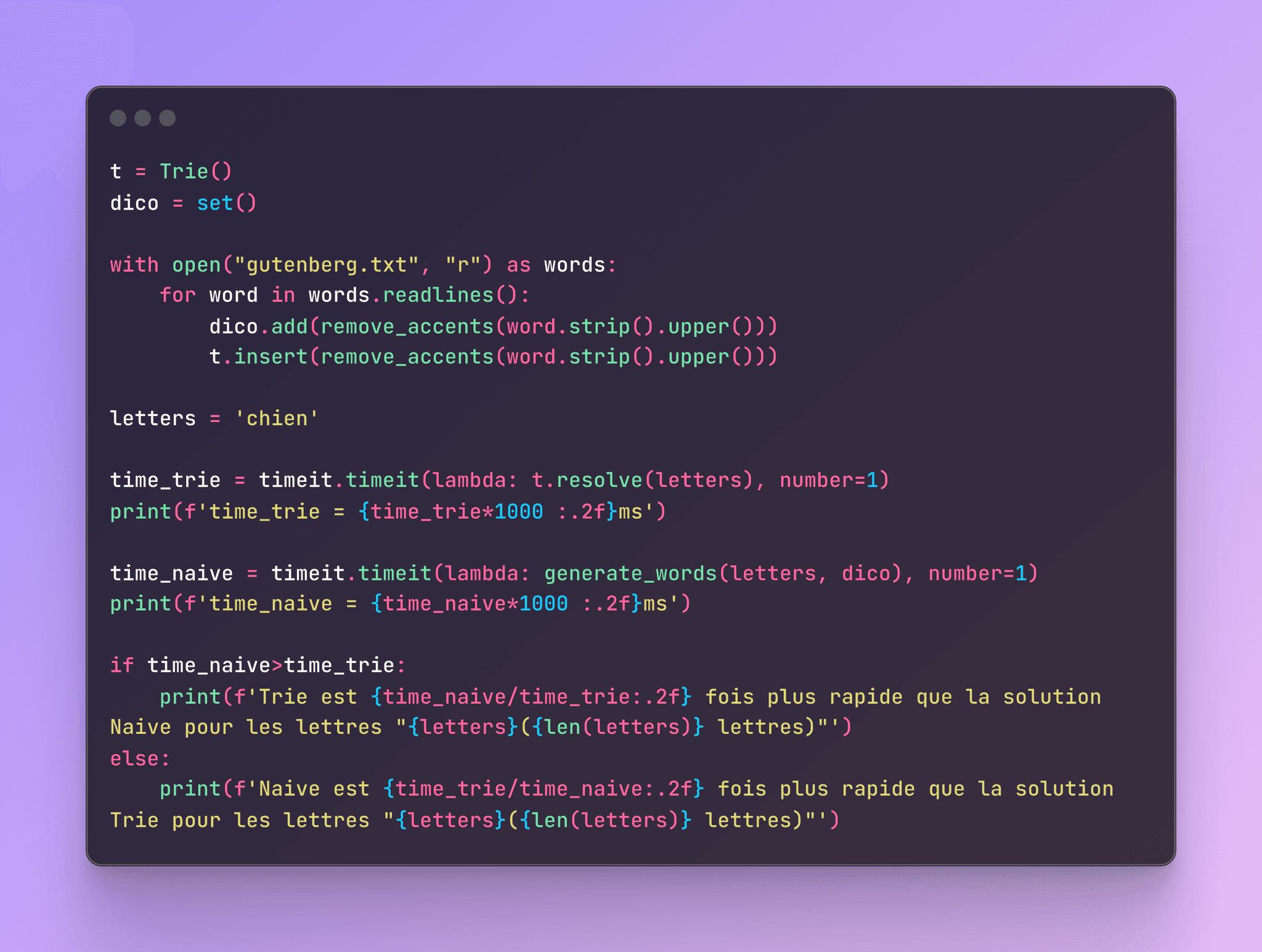
`gutenberg.txt` est un fichier contenant environ 300 000 mots en français, et `remove_accents` est une fonction qui retire les accents. Je vous fais confiance, vous trouverez ça facilement ailleurs.

Pour les lettres C-H-I-E-N, voilà le résultat :

time_trie = 0.13ms time_naive = 0.15ms Trie est 1.09 fois plus rapide que la solution Naive pour les lettres "chien"

QUOI ? C'EST TOUT ??? J'AI FAIT TOUT ÇA POUR SI PEU !

Je réalise que, pour l'usage que j'en avais — résoudre un simple jeu de mots — utiliser un algorithme sophistiqué comme le Trie m'a en fait fait perdre mon temps... Bon, je vais aller fumer une cigarette pour me détendre.

Après une petite pause pour reprendre mes esprits, je me rends compte que même si l'amélioration n'était pas spectaculaire pour un simple jeu de mots, j'ai tout de même enrichi ma boîte à outils algorithmique. 

Maintenant, voyons ce que ça donne avec un plus grand nombre de lettres :

time_trie = 0.17ms time_naive = 0.66ms Trie est 3.81 fois plus rapide que la solution Naive pour les lettres : "batman (6 lettres)"

time_trie*1000 = 0.99ms time_naive*1000 = 59.21ms Trie est 59.68 fois plus rapide que la solution Naive pour les lettres : "superman (8 lettres)"

time_trie = 1.02ms time_naive = 434.61ms Trie est 424.55 fois plus rapide que la solution Naive pour les lettres : "supernany (9 lettres)"

time_trie = 2.21ms time_naive =4546.19ms Trie est 2059.54 fois plus rapide que la solution Naive pour les lettres : "superwoman (10 lettres)"

time_trie = 4.59ms time_naive =53396.14ms Trie est 11635.96 fois plus rapide que la solution Naive pour les lettres : "spiderwoman (11 lettres)"

Analyse des résultats

Les chiffres parlent d’eux-mêmes : à partir de 6 lettres, le Trie prend nettement l’avantage. Pour des mots de plus de 10 lettres, l’approche naïve devient tout simplement inapplicable.

Il est vrai que pour mon petit jeu, le Trie peut sembler un peu excessif. Mais imaginez que je veuille étendre mon solveur pour une application web avec de nombreux utilisateurs : c’est là que le Trie ferait toute la différence.

Pour résumer, ce projet m’a vraiment aidé à reprendre le contrôle sur mon temps. J’ai réussi à mettre de côté cette addiction au jeu Mots de lettres et, en prime, à regagner un temps que je pensais perdu à jamais. Mais, comme toujours, alors qu’on pense avoir résolu un problème, un autre surgit. Alors que je pensais maîtriser la situation, une nouvelle addiction est apparue : la cigarette. Oui, j’ai échangé une obsession pour une autre, mais au moins, cette fois, j’ai enrichi mes compétences en algorithmie et appris à mieux gérer mon temps.

En somme, la bataille continue, et qui sait, ma prochaine mission pourrait bien être de trouver un moyen de fumer moins. C’est pas gagné, mais bon, ça fait partie du défi, n'est-ce pas ?